- Calculators
- ::
- 2D Shapes
- ::
- Rectangle Calculator
Rectangle calculator
The rectangle solver finds missing width, length, diagonal, area or perimeter of a rectangle. The calculator accepts all types of input values, including fractions and square roots, and provides step-by-step explanation.
Find the diagonal $ d $ of a rectangle if side $a = \frac{ 3 }{ 2 }$ and perimeter $P = \frac{ 11 }{ 2 }$.
solution
$$ d = \frac{\sqrt{ 61 }}{ 4 } $$explanation
STEP 1: find side $ b $
To find side $ b $ use formula:
$$ P = 2 a + 2 b $$After substituting $ P = \frac{ 11 }{ 2 } $ and $ a = \frac{ 3 }{ 2 } $ we have:
$$ \frac{ 11 }{ 2 } = 2 \cdot \frac{ 3 }{ 2 } + 2 b $$ $$ \frac{ 11 }{ 2 } = 3 + 2 b $$ $$ 2 b = \frac{ 11 }{ 2 } - 3 $$ $$ 2 b = \frac{ 5 }{ 2 } $$ $$ b = \dfrac{ \frac{ 5 }{ 2 } }{ 2 } $$ $$ b = \frac{ 5 }{ 4 } $$STEP 2: find diagonal $ d $
To find diagonal $ d $ use Pythagorean Theorem:
$$ a^2 + b^2 = d^2 $$After substituting $ a = \frac{ 3 }{ 2 } $ and $ b = \frac{ 5 }{ 4 } $ we have:
$$ \left(\frac{ 3 }{ 2 }\right)^2 + \left(\frac{ 5 }{ 4 }\right)^2 = d^2 $$ $$ \frac{ 9 }{ 4 } + \frac{ 25 }{ 16 } = d^2 $$ $$ d^2 = \frac{ 61 }{ 16 } $$ $$ d = \sqrt{ \frac{ 61 }{ 16 } } $$$$ d = \frac{\sqrt{ 61 }}{ 4 } $$
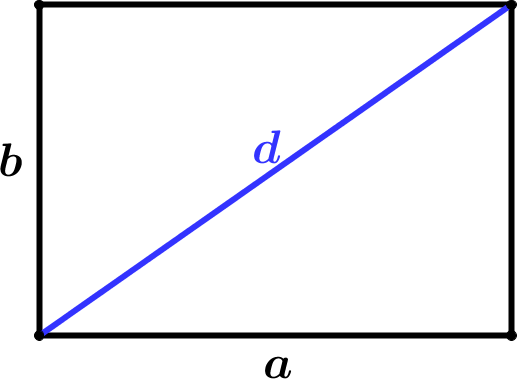
| $$ A = ab $$ |
| area |
| $$ P = 2a + 2b $$ |
| perimeter |
| $$ d^2 = a^2 + b^2 $$ |
| diagonal |
Rectangle calculations
This calculator uses the following formulas to find the missing values of a rectangle:
| Area: | $$ A = a \cdot b $$ |  |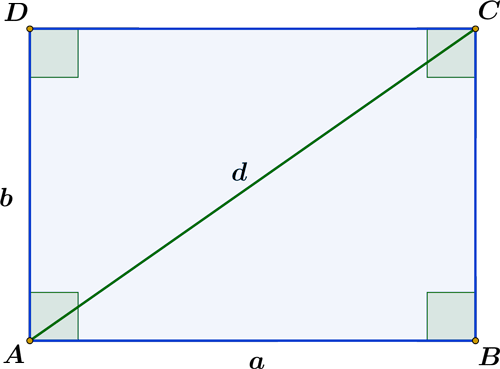
| Perimeter: | $$ P = 2a + 2b $$ | |
| Diagonal: | $$ d^2 = a^2 + b^2 $$ |
Example 01 :
What is the area of a rectangle with a base of 12 cm and a height of 3/2 cm?
Solution:
base $ a = 6 $
height $ b = \dfrac{9}{2} $
$$ \color{blue}{A = a \cdot b} = 6 \cdot \frac{9}{2} = \frac{54}{2} = 27 $$Example 02 :
What is the perimeter of a rectangle with a length of 7/2cm and a width of 5/2cm?
Solution:
length $ a = \dfrac{7}{2} \, cm $
width $ b = \dfrac{5}{2} \, cm $
$$ \color{blue}{P = 2a + 2b} = 2 \cdot \frac{7}{2} + 2 \cdot \dfrac{5}{2} = 7 + 5 = 12 $$Example 03 :
The area of a rectangle is 42 cm2. Find its perimeter if the width is 7cm.
Solution:
We'll need two steps to solve this one:
Step 1: find length ( b ):
width $ a = 7 cm $
area: $ A = 42 cm $
$$ \begin{aligned} A & = a \cdot b \\[ 1 em] 42 & = 7 \cdot b \\[ 1 em] b & = \frac{42}{7}\\[ 1 em] b & = 6 \\[ 1 em] \end{aligned} $$Step 2: find perimeter ( P )
width $ a = 7 cm $
length $ b = 6 cm $
$$ \begin{aligned} P & = 2a + 2b \\[ 1 em] P & = 2 \cdot 7 + 2 \cdot 6 \\[ 1 em] P & = 14 + 12 \\[ 1 em] P & = 28 \, cm^2 \\[ 1 em] \end{aligned} $$Example 04 :
What is the diagonal of a rectangle if the perimeter is P = 11/2 cm and a width is a = 3/2 cm ?
Solution:
Step 1: find length ( b ):
width $ a = \dfrac{3}{2} cm $
perimeter: $ P = \dfrac{11}{2} cm $
$$ \begin{aligned} P & = 2a + 2b \\[ 1 em] \frac{11}{2} & = 2 \cdot \frac{3}{2} + 2b \\[ 1 em] \frac{11}{2} & = 3 + 2b \\[ 1 em] 2b &= \frac{11}{2} - 3 \\[1 em] 2b &= \frac{5}{2} \\[1 em] b &= \frac{5}{4} \end{aligned} $$Step 2: find diagonal ( d )
width $ a = \dfrac{3}{2} cm $
length $ b = \dfrac{5}{4} cm $
$$ \begin{aligned} d^2 & = a^2 + b^2 \\[ 1 em] d^2 & = \left( \frac{3}{2} \right)^2 + \left( \frac{5}{4} \right)^2 \\[ 1 em] d^2 & = \frac{9}{4} + \frac{25}{16} \\[ 1 em] d^2 & = \frac{61}{16} \\[ 1 em] d & = \frac{\sqrt{61}}{4} \end{aligned} $$