- Calculators
- ::
- 2D Shapes
- ::
- Triangle Calculator
Triangle calculator
This solver uses the Law of Sines, and the Law of Cosines to solve acute and obtuse triangles , i.e., to find missing angles or sides if you know any three of them. Provide any three triangle properties of an oblique triangle to find the missing side, angle or area. The calculator shows all the steps and gives a full explanation for each step.
working...
Oblique triangle formulas
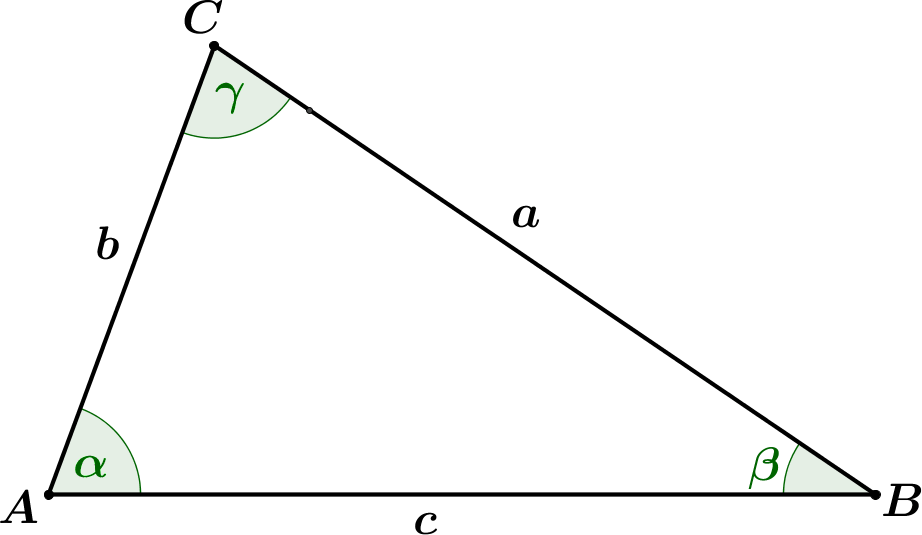
| $$ A = \frac{a\,b\,\sin\gamma}{2} $$ |
| area |
| $$ A = \frac{b\,c\,\sin\alpha}{2} $$ |
| area |
| $$ A = \frac{a\,c\,\sin\beta}{2} $$ |
| area |
| $$ c^2 = a^2 + b^2 - 2ab \cos \gamma $$ |
| law of cosines |
| $$ b^2 = a^2 + c^2 - 2ac \cos \beta $$ |
| law of cosines |
| $$ a^2 = b^2 + c^2 - 2 b c \cos \alpha $$ |
| law of cosines |
| $$ \frac{a}{\sin\alpha} = \frac{b}{\sin\beta} = \frac{c}{\sin\gamma} $$ |
| law of sines |
Examples
ex 1:
A triangle has sides equal to 3m, 5m and 6m. Find angle &alpha using cosine theorem.
ex 2:
Find the area of a triangle using Herons formula if the lengths of a sides are a=13cm, b=14cm and =15cm.
ex 3:
If a=12in, b=18in and angle β=45º, find the angle α using the sine theorem.
ex 4:
Use the Cosine theorem to find the side c of a triangle ABC if a=12cm, b=8cm and γ=60o
Related calculators
Find more worked-out examples in our database of solved problems.
Search our database with more than 300 calculators
452 861 664 solved problems
×
ans:
syntax error
C
DEL
ANS
±
(
)
÷
×
7
8
9
–
4
5
6
+
1
2
3
=
0
.