Math Calculators, Lessons and Formulas

It is time to solve your math problem

mathportal.org

Circle calculator

google play badge app store badge

This calculator computes the area, circumference, radius and diameter of a circle. The calculator provides a step-by-step explanation to find the unknown element.

Circle Calculator
Input one element of a circle and select element to find.
help ↓↓ examples ↓↓
Solve for
Enter one element of a circle.
A =
C =
r =
d =
thumb_up 273 thumb_down

Get Widget Code

working...
Numbers
Polynomials
Rational Expressions
Radicals
Solving Equations
Quadratic Equation
2D Shapes
3D Shapes
Analytic geometry
Complex Numbers
Systems of equations
Matrices
Calculus Calculators
Sequences & Series
Trigonometry
Statistics and probability
Financial Calculators
Other Calculators

Hire MATHPORTAL experts to do math homework for you.

Prices start at $3 per problem.

Circle formulas
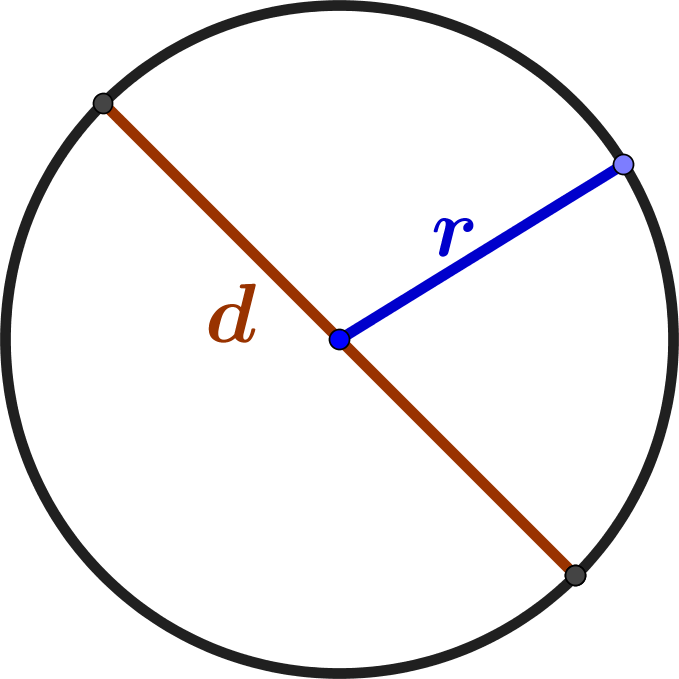
Circle illustration showing radius, diameter and area.
$$ A = r^2 \, \times \pi $$
area
$$ C = 2 \, r \, \pi $$
perimeter
$$ d = 2 \, r $$
diameter
Examples
ex 1:
Find the area of the circle with a diameter of 6cm.
ex 2:
Calculate the area of a circle whose circumference is C=6π.
ex 3:
Find the diameter of a circle with an area of A = 9/4πin.
Find more worked-out examples in our database of solved problems.
Search our database with more than 300 calculators
×

Circle calculator – Widget Code

Feel free to copy the widget code below and paste it into your website or blog. The widget will look like the example below.

Widget preview: Circle calculator

Copy code to clipboard

452 861 664 solved problems
×
ans:
syntax error
C
DEL
ANS
±
(
)
÷
×
7
8
9
–
4
5
6
+
1
2
3
=
0
.