Determinant Calculator
This calculator computes the determinant of a square matrix. The calculator shows all steps with a detailed explanation.
Tutorial
The determinant is a number that we can calculate from any square matrix.
Why do we use determinants?
We use determinants to:
1. Find out if the matrix has an inverse.
2. Find an inverse of a square matrix.
3. Solve the system of linear equations.
4. Find the characteristic polynomial, eigenvalues and eigenvectors.
Determinant 2 x 2
For any matrix with 2 rows and 2 columns, the determinant can be calculated using the formula:

Example
Find the determinant of $ A = \begin{bmatrix} 4 & -3 \\ 2 & 3 \end{bmatrix}$
Using the above formula, we have:
|A| = 4·3-(-3)·2 =
= 12 + 6 = 18
Determinant 3 x 3
The determinant of a 3x3 matrix can be solved using the determinants of the 2x2 matrices using the formula:
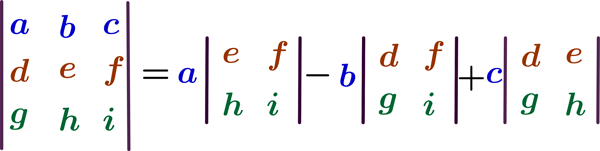
Example
Find the determinant of $ A = \begin{bmatrix} 2 & 0 & 6 \\ 3 & 2 & 1 \\ 0 & 4 & 8 \end{bmatrix}$
Using the determinant formula for 3x3 matrices, we have
$$\begin{aligned} A &= \begin{bmatrix} 2 & 0 & 6 \\ 3 & 2 & 1 \\ 0 & 4 & 8 \end{bmatrix} = \\[2 em] &= 2 \cdot \begin{bmatrix} 2 & 1 \\ 4 & 8 \end{bmatrix} - 0 \cdot \begin{bmatrix} 3 & 2 \\ 1 & 8 \end{bmatrix} + 6 \cdot \begin{bmatrix} 3 & 2 \\ 0 & 4 \end{bmatrix} = \\[2 em] &= 2 \cdot 12 - 0 \cdot 22 + 6 \cdot 12 = 96 \end{aligned} $$