- Calculators
- ::
- Matrices and Vectors
- ::
- Vector Calculator
Vector calculator
This calculator performs all vector operations in two- and three-dimensional space. You can add, subtract, find length, find vector projections, and find the dot and cross product of two vectors. For each operation, the calculator writes a step-by-step, easy-to-understand explanation of how the work has been done.
Vector operations
In this tutorial, we'll learn how to find: magnitude, dot product, angle between two vectors and cross product of two vectors.
1 : Magnitude
Magnitude is the vector length. The formula for the magnitude of a vector $\vec{v} = (v_1, v_2) $ is:
$$ \| \vec{v} \| = \sqrt{v_1^2 + v_2^2 } $$Example 01: Find the magnitude of the vector $ \vec{v} = (4, 2) $.
In this example we have $ v_1 = 4 $ and $ v_2 = 2 $ so the magnitude is:
$$ \| \vec{v} \| = \sqrt{4^2 + 2 ^2} = \sqrt{20} = 2\sqrt{5} $$
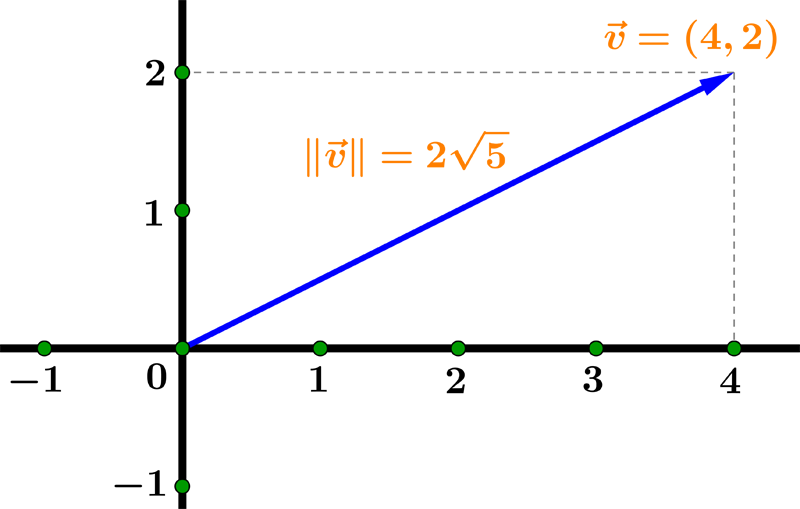
Example 02: Find the magnitude of the vector $ \vec{v} = \left(\dfrac{2}{3}, \sqrt{3}, 2\right) $.
2 : Dot product
The formula for the dot product of vectors $ \vec{v} = (v_1, v_2) $ and $ \vec{w} = (w_1, w_2) $ is
$$ \vec{v} \cdot \vec{w}= v_1 \cdot w_1 + v_2 \cdot w_2 $$Two vectors are orthogonal to each other if their dot product is equal zero.
Example 03: Calculate the dot product of $ \vec{v} = \left(4, 1 \right) $ and $ \vec{w} = \left(-1, 5 \right) $. Check if the vectors are mutually orthogonal.
To find the dot product we use the component formula:
$$ \begin{aligned} \vec{v} \cdot \vec{w} &= \left(4, 1 \right) \cdot \left(-1, 5 \right) = \\[1 em] &= 4 \cdot (-1) + 1 \cdot 5 = -4 + 5 = 1 \end{aligned} $$
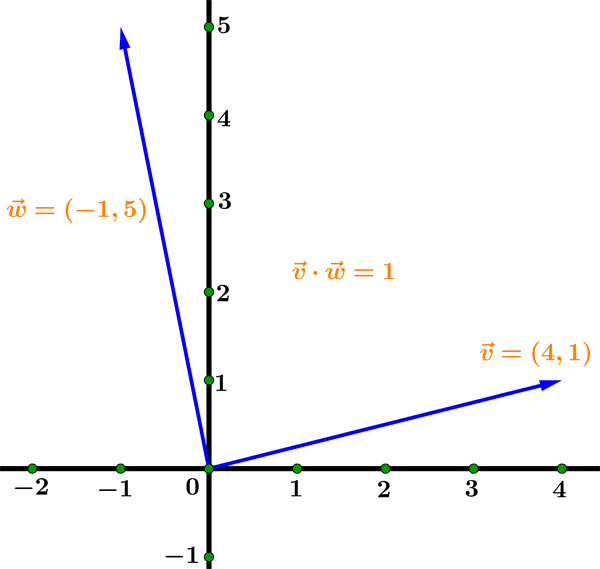
Since the dot product is not equal to zero, we can conclude that vectors ARE NOT orthogonal.
Example 04: Find the dot product of the vectors $ \vec{v_1} = \left(\dfrac{1}{2}, \sqrt{3}, 5 \right) $ and $ \vec{v_2} = \left( 4, -\sqrt{3}, 10 \right) $.
3 : Angle between two vectors
To find the angle $ \alpha $ between vectors $ \vec{a} $ and $ \vec{b} $, we use the following formula:
$$ \cos \alpha = \dfrac{\vec{a} \cdot \vec{b}}{ \|\vec{a}\| \, \|\vec{b}\|} $$Note that $ \vec{a} \cdot \vec{b} $ is a dot product while $\|\vec{a}\|$ and $\|\vec{b}\|$ are magnitudes of vectors $ \vec{a} $ and $ \vec{b}$.
Example 05: Find the angle between vectors $ \vec{a} = ( 4, 3) $ and $ \vec{b} = (-2, 2) $.
First we will find the dot product and magnitudes:
$$ \begin{aligned} \vec{a} \cdot \vec{b} &= ( 4, 3) \cdot (-2, 2) = 4 \cdot (-2) + 3 \cdot 2 = -2 \\[1 em] \| \vec{a} \| &= \sqrt{4^2 + 3^2} = \sqrt{16 + 9} = \sqrt{25} = 5 \\[1 em] \| \vec{b} \| &= \sqrt{(-2)^2 + 2^2} = \sqrt{4 + 4} = \sqrt{8} \end{aligned} $$Now we'll find the $ \cos \alpha $
$$ \cos \alpha = \dfrac{\vec{a} \cdot \vec{b}}{ \|\vec{a}\| \, \|\vec{b}\|} = \dfrac{-2}{5 \sqrt{8}} \approx -0.1414 $$The angle $ \alpha $ is:
$$ \alpha = \cos^{-1}(-0.1414) \approx 98^{o} $$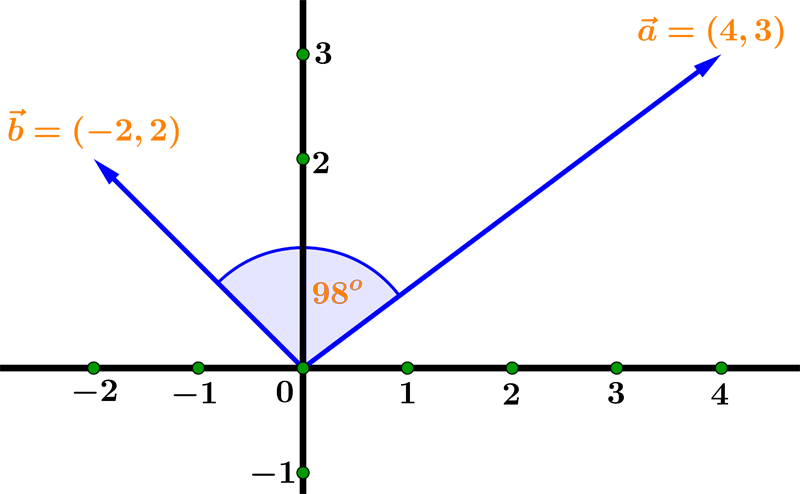
Example 06: Find the angle between vectors $ \vec{v_1} = \left(2, 1, -4 \right) $ and $ \vec{v_2} = \left( 3, -5, 2 \right) $.
4 : Cross product
The cross product of vectors $ \vec{v} = (v_1,v_2,v_3) $ and $ \vec{w} = (w_1,w_2,w_3) $ is given by the formula:
$$ \vec{v} \times \vec{w} = \left( v_2 w_3 - v_3 w_2, v_3 w_1 - v_1 w_3, v_1 w_2 - v_2 w_1 \right) $$Note that the cross product requires both vectors to be three-dimensional.
If the two vectors are parallel than the cross product is equal zero.
Example 07: Find the cross products of the vectors $ \vec{v} = ( -2, 3 , 1) $ and $ \vec{w} = (4, -6, -2) $. Check if the vectors are parallel.
We'll find cross product using above formula
v • w =
= (3×(-2)-1×(-6), 1×4-(-2)×(-2), -2×(-6)-3×4) =
= (0, 0, 0)
Since the cross product is zero, we conclude that the vectors are parallel.
Example 08: Find the cross products of the vectors $ \vec{v_1} = \left(4, 2, -\dfrac{3}{2} \right) $ and $ \vec{v_2} = \left(\dfrac{1}{2}, 0, 2 \right) $.