- Calculators
- ::
- Financial Calculators
- ::
- Compound Interest Calculator
Compound interest calculator
Compound interest is calculated on both the initial payment, and the interest earned in previous periods.
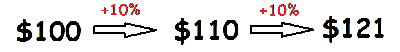
working...
Examples
ex 1:
What is the value of a $4500 deposit at 7% compounded annual interest if it is held in a
bank for 9 years?
ex 2:
What will a $3500 deposit at 10% compounded
monthly be worth after 8 years in the bank?
ex 3:
How much money would you need to put today at 8% annual
compounded monthly
interest to have $1200 in the account after 12 years?
ex 4:
Determine the present value of $1000 at a 12% annual interest rate compounded
quarterly at the end of two years.
ex 5:
What is the estimated yearly interest rate if you give someone
$1700 and get repaid
$1910 in two years?
ex 6:
Assume that a savings account with a principal of $1350 is
compounded monthly.
After 8 months, the total had risen to $1424. What was the interest rate per year?
ex 7:
How long does it take $4300 to grow to $6720 when compounded quarterly at
9%?
Related calculators
Search our database with more than 300 calculators
452 861 664 solved problems
×
ans:
syntax error
C
DEL
ANS
±
(
)
÷
×
7
8
9
–
4
5
6
+
1
2
3
=
0
.