Complex number calculator

1 : Modulus ( Magnitude )

The modulus or magnitude of a complex number ( denoted by $ \color{blue}{ | z | }$ ), is the distance between the origin and that number.

If the $ z = a + bi $ is a complex number than the modulus is

$$ |z| = \sqrt{a^2 + b^2} $$

Example 01: Find the modulus of $ z = \color{blue}{6} + \color{purple}3{} i $.

In this example $ \color{blue}{a = 6} $ and $ \color{purple}{b = 3} $, so the modulus is:

$$ \begin{aligned} | z | &= \sqrt{ a^2 + b^2} = \sqrt{6^2 + 3^2} = \\[1 em] &= \sqrt{36 + 9} = \sqrt{45} = \\[1 em] &= \sqrt{9 \cdot 5} = 3 \sqrt{5} \end{aligned} $$

2 : Conjugate

To find the complex conjugate of a complex number, we need to change the sign of the imaginary part. The conjugate of $ z = a \color{red}{ + b}\,i $ is:

$$ \overline{z} = a \color{red}{ - b}\,i $$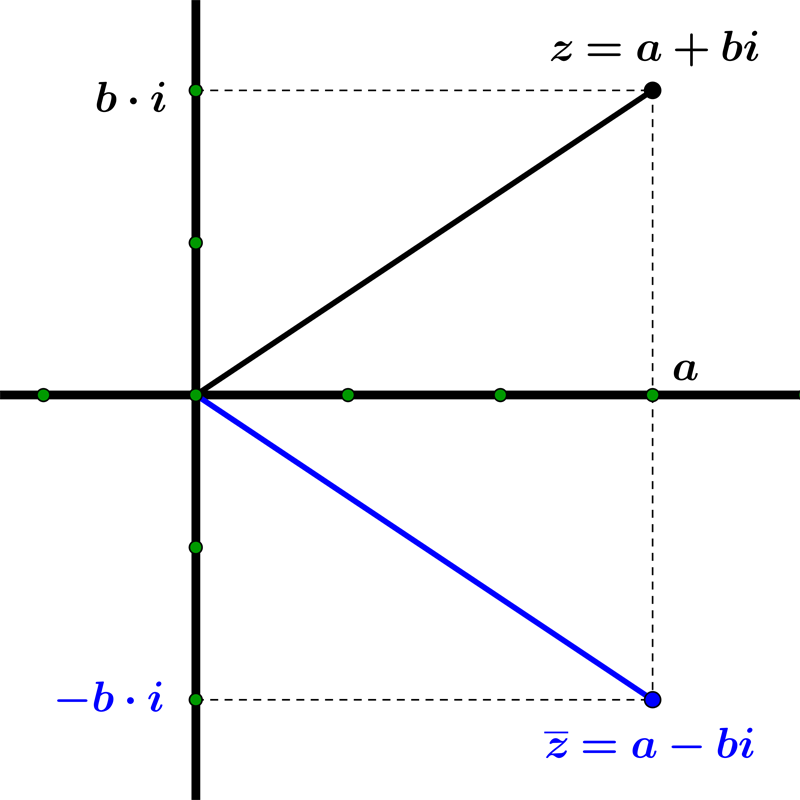

Example 02: The complex conjugate of $~ z = 3 \color{blue}{+} 4i ~$ is $~ \overline{z} = 3 \color{red}{-} 4i $.

Example 03: The conjugate of $~ z = - 4i ~$ is $~ \overline{z} = 4i $.

Example 04: The conjugate of $~ z = 15 ~$ is $~ \overline{z} = 15 ~$, too.

4 : Inverse

The inverse or reciprocal of a complex number $ a + b\,i $ is

$$ \color{blue}{ \frac{1}{a + b\,i}} $$

Here is an example of how to find the inverse.

Example 06: Find the inverse of the number $ z = 4 + 3i $

$$ \begin{aligned} \frac{1}{z} &= \frac{1}{4+3i} = \frac{1}{4+3i} \cdot \frac{4-3i}{4-3i} = \\[1 em] &= \frac{4-3i}{(4+3i)(4-3i)} = \frac{4-3i}{4^2 - (3i)^2} = \\[1 em] &= \frac{4-3i}{16+9} = \frac{4-3i}{25} = \frac{4}{25} - \frac{3}{25} i \end{aligned} $$

3 : Polar Form

The polar form of a complex number $ z = a + i\,b$ is given as $ z = |z| ( \cos \alpha + i \sin \alpha) $.

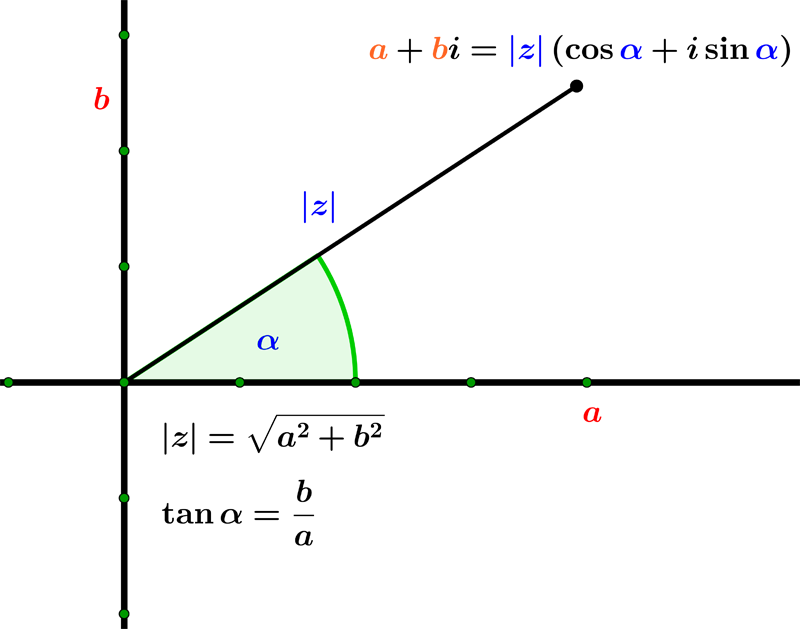
Example 05: Express the complex number $ z = 2 + i $ in polar form.

To find a polar form, we need to calculate $|z|$ and $ \alpha $ using formulas in the above image.

$$ |z| = \sqrt{2^2 + 1^2} = \sqrt{5}$$ $$ \tan \alpha = \dfrac{b}{a} = \dfrac{1}{2} \implies \alpha = \tan^{-1}\left(\dfrac{1}{2}\right) \approx 27^{o} $$

So, the polar form is:

$$ z = \sqrt{5} \left( \cos 27^{o} + i \sin27^{o} \right) $$