- Calculators
- ::
- Complex numbers
- ::
- Modulus, Inverse, Polar Form,...
Complex number calculator
The calculator does the following: extracts the square root, calculates the modulus, finds the inverse, finds conjugate and transforms complex numbers into polar form. For each operation, the solver provides a detailed step-by-step explanation.
Find the modulus of
$$ z = 2+i $$solution
The polar form of $ z $ is:
$$ z = \sqrt{ 5 } \cdot \left ( cos ~ 27^o + i \cdot sin ~ 27^o \right) $$explanation
The polar form of the complex number $ z = a + bi$ is:
$$ z = r \cdot \left(cos~\theta + i \cdot sin ~ \theta \right) $$where, $ r $ is the modulus of $ z $ and $~ \theta ~$ is an argument of $ z $.
The moduo for $ a = 2 $ and $ b = 1 $ is:
$$ r = \sqrt{a^2 + b^2} = \cdots =\sqrt{ 5 } $$To find argument $ \theta $ we use one of the following formulas:
$$ \begin{aligned} \theta & = \arctan \left( \frac{b}{a} \right) \text{ if } a > 0 \\ \theta & = \arctan \left( \frac{b}{a} \right) + 180^o \text{ if } a < 0 \\ \\ \theta & = 90^o \text{ if } a = 0 \text{ and } b > 0 \\ \\ \theta & = 270^o \text{ if } a = 0 \text{ and } b < 0 \end{aligned} $$In this example: $ a = 2 $ and $ b = 1 $ so:
$$ \theta = arctan \left( \frac{b}{a} \right) $$$$ \theta = arctan \left( \frac{ 1 }{ 2 } \right) $$$$ \theta = arctan \left( \frac{ 1 }{ 2 } \right) $$$$ \theta \approx 27^o $$Operations on complex numbers
This calculator performs five operations on a single complex number.
It computes module, conjugate, inverse, roots and polar form.
1 : Modulus ( Magnitude )
The modulus or magnitude of a complex number ( denoted by $ \color{blue}{ | z | }$ ), is the distance between the origin and that number.
If the $ z = a + bi $ is a complex number than the modulus is
$$ |z| = \sqrt{a^2 + b^2} $$
Example 01: Find the modulus of $ z = \color{blue}{6} + \color{purple}3{} i $.
In this example $ \color{blue}{a = 6} $ and $ \color{purple}{b = 3} $, so the modulus is:
$$ \begin{aligned} | z | &= \sqrt{ a^2 + b^2} = \sqrt{6^2 + 3^2} = \\[1 em] &= \sqrt{36 + 9} = \sqrt{45} = \\[1 em] &= \sqrt{9 \cdot 5} = 3 \sqrt{5} \end{aligned} $$2 : Conjugate
To find the complex conjugate of a complex number, we need to change the sign of the imaginary part. The conjugate of $ z = a \color{red}{ + b}\,i $ is:
$$ \overline{z} = a \color{red}{ - b}\,i $$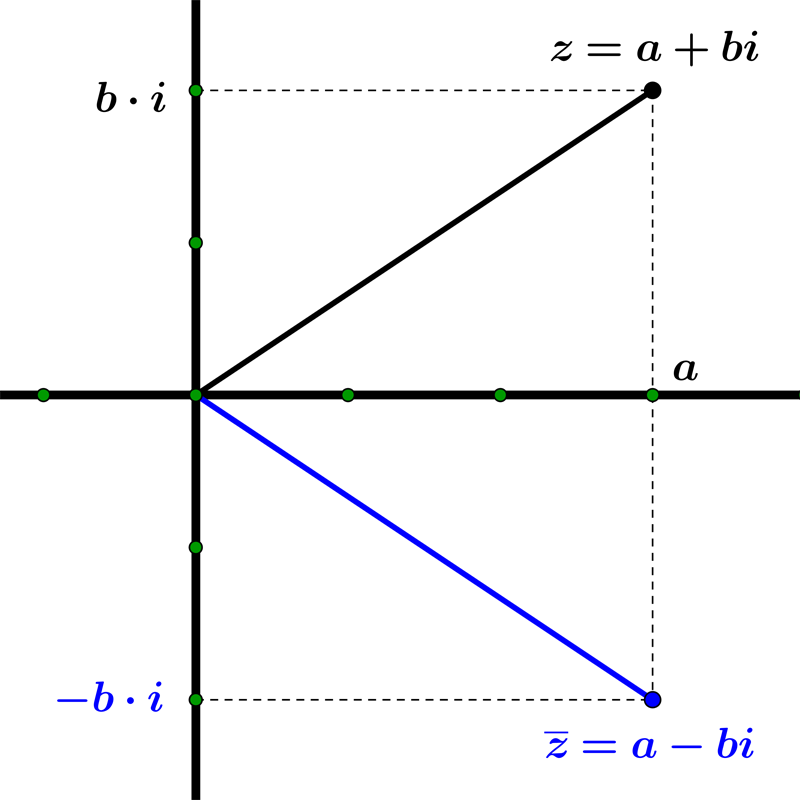
Example 02: The complex conjugate of $~ z = 3 \color{blue}{+} 4i ~$ is $~ \overline{z} = 3 \color{red}{-} 4i $.
Example 03: The conjugate of $~ z = - 4i ~$ is $~ \overline{z} = 4i $.
Example 04: The conjugate of $~ z = 15 ~$ is $~ \overline{z} = 15 ~$, too.
4 : Inverse
The inverse or reciprocal of a complex number $ a + b\,i $ is
$$ \color{blue}{ \frac{1}{a + b\,i}} $$Here is an example of how to find the inverse.
Example 06: Find the inverse of the number $ z = 4 + 3i $
$$ \begin{aligned} \frac{1}{z} &= \frac{1}{4+3i} = \frac{1}{4+3i} \cdot \frac{4-3i}{4-3i} = \\[1 em] &= \frac{4-3i}{(4+3i)(4-3i)} = \frac{4-3i}{4^2 - (3i)^2} = \\[1 em] &= \frac{4-3i}{16+9} = \frac{4-3i}{25} = \frac{4}{25} - \frac{3}{25} i \end{aligned} $$3 : Polar Form
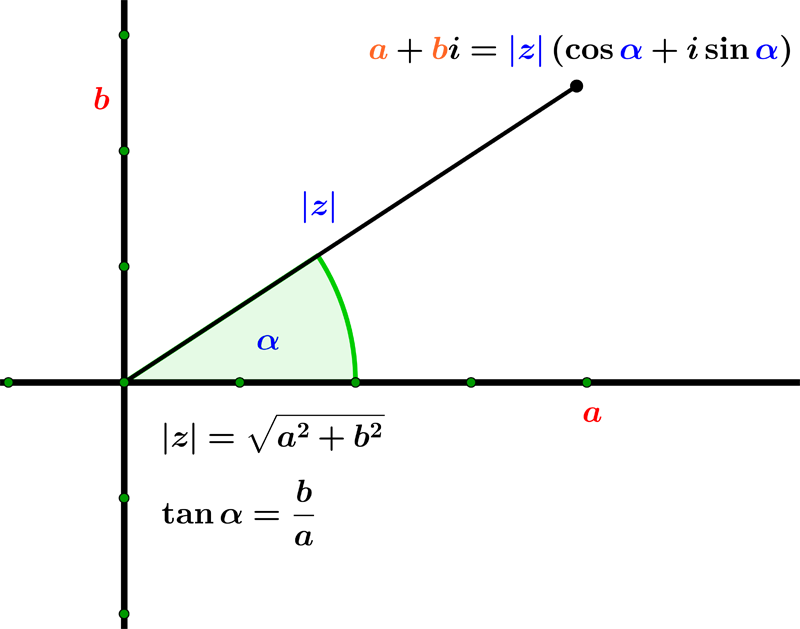
The polar form of a complex number $ z = a + i\,b$ is given as $ z = |z| ( \cos \alpha + i \sin \alpha) $.
Example 05: Express the complex number $ z = 2 + i $ in polar form.
To find a polar form, we need to calculate $|z|$ and $ \alpha $ using formulas in the above image.
$$ |z| = \sqrt{2^2 + 1^2} = \sqrt{5}$$ $$ \tan \alpha = \dfrac{b}{a} = \dfrac{1}{2} \implies \alpha = \tan^{-1}\left(\dfrac{1}{2}\right) \approx 27^{o} $$So, the polar form is:
$$ z = \sqrt{5} \left( \cos 27^{o} + i \sin27^{o} \right) $$Please tell me how can I make this better.

