- Calculators
- ::
- Matrices and Vectors
- ::
- Vector Calculator
Vector calculator
This calculator performs all vector operations in two and three dimensional space.
You can add, subtract, find length, find vector projections, find dot and cross product of two vectors.
For each operation, calculator writes a step-by-step, easy to understand
explanation on how the work has been done.
Find the angle between vectors $ \left(2,~1,~-4\right)$ and $\left(3,~-5,~2\right)$.
solution
$$ \measuredangle \left(v_1, v_2 \right) = 104.347^o $$explanation
The angle between vectors $ \vec{a} $ and $ \vec{b} $ is given by
$$ \cos(\Theta) = \frac{ \vec{a} \cdot \vec{b} }{ \| \vec{a} \| \cdot \| \vec{b} \| } $$First we will find the dot product and magnitudes:
$$ \begin{aligned}\vec{a} \cdot \vec{b} &= -7 \\[1 em]\| \vec{a} \| &= \sqrt{ 21 } \\[1 em]\| \vec{b} \| &= \sqrt{ 38 } \\[1 em]\end{aligned} $$Now we can find $ \cos \Theta $
$$ cos(\Theta) = \frac{ \vec{a} \cdot \vec{b} }{ \| \vec{a} \| \cdot \| \vec{b} \| } = \frac{ -7 }{ \sqrt{ 21 } \cdot \sqrt{ 38 } } = - \frac{\sqrt{ 798 }}{ 114 } $$Now we 'll find $ \Theta $
$$ \Theta = \arccos \left( - \frac{\sqrt{ 798 }}{ 114 } \right) \approx 104.347^o $$Vector operations
In this tutorial we'll learn how to find: magnitude, dot product, angle between two vectors and cross product of two vectors.
1 : Magnitude
Magnitude is the vector length. The formula for magnitude of a vector $ \vec{v} = (v_1, v_2) $ is:
$$ \| \vec{v} \| = \sqrt{v_1^2 + v_2^2 } $$Example 01: Find the magnitude of the vector $ \vec{v} = (4, 2) $.
In this example we have $ v_1 = 4 $ and $ v_2 = 2 $ so the magnitude is:
$$ \| \vec{v} \| = \sqrt{4^2 + 2 ^2} = \sqrt{20} = 2\sqrt{5} $$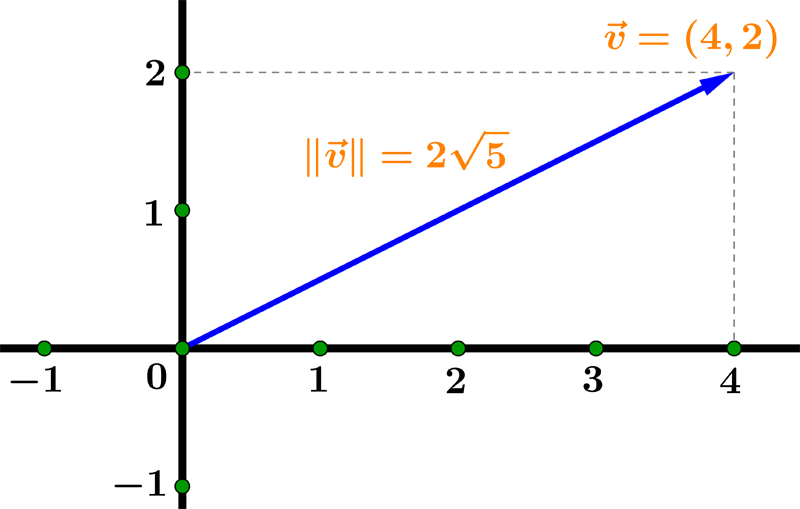
Example 02: Find the magnitude of the vector $ \vec{v} = \left(\dfrac{2}{3}, \sqrt{3}, 2\right) $.
2 : Dot product
The formula for the dot product of vectors $ \vec{v} = (v_1, v_2) $ and $ \vec{w} = (w_1, w_2) $ is
$$ \vec{v} \cdot \vec{w}= v_1 \cdot w_1 + v_2 \cdot w_2 $$Two vectors are orthogonal to each other if their dot product is equal zero.
Example 03: Calculate the dot product of $ \vec{v} = \left(4, 1 \right) $ and $ \vec{w} = \left(-1, 5 \right) $. Check if the vectors are mutually orthogonal.
To find the dot product we use the component formula:
$$ \begin{aligned} \vec{v} \cdot \vec{w} &= \left(4, 1 \right) \cdot \left(-1, 5 \right) = \\[1 em] &= 4 \cdot (-1) + 1 \cdot 5 = -4 + 5 = 1 \end{aligned} $$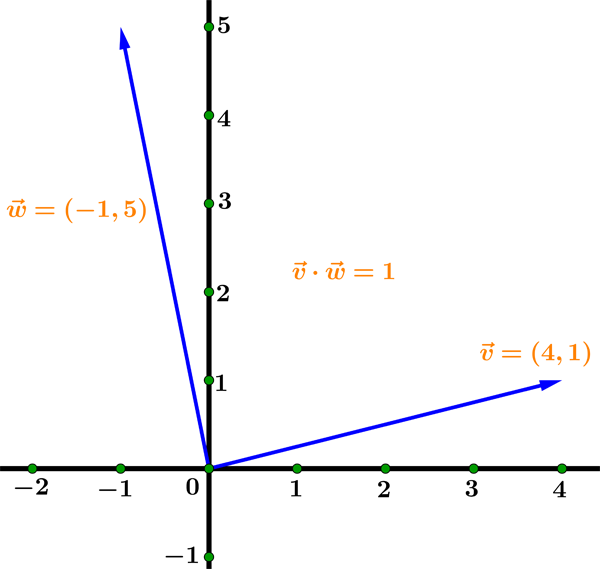
Since the dot product is not equal zero we can conclude that vectors ARE NOT orthogonal.
Example 04: Find the dot product of the vectors $ \vec{v_1} = \left(\dfrac{1}{2}, \sqrt{3}, 5 \right) $ and $ \vec{v_2} = \left( 4, -\sqrt{3}, 10 \right) $.
3 : Angle between two vectors
To find the angle $ \alpha $ between vectors $ \vec{a} $ and $ \vec{b} $, we use the following formula:
$$ \cos \alpha = \dfrac{\vec{a} \cdot \vec{b}}{ \|\vec{a}\| \, \|\vec{b}\|} $$Note that $ \vec{a} \cdot \vec{b} $ is a dot product while $\|\vec{a}\|$ and $\|\vec{b}\|$ are magnitudes of vectors $ \vec{a} $ and $ \vec{b}$.
Example 05: Find the angle between vectors $ \vec{a} = ( 4, 3) $ and $ \vec{b} = (-2, 2) $.
First we will find the dot product and magnitudes:
$$ \begin{aligned} \vec{a} \cdot \vec{b} &= ( 4, 3) \cdot (-2, 2) = 4 \cdot (-2) + 3 \cdot 2 = -2 \\[1 em] \| \vec{a} \| &= \sqrt{4^2 + 3^2} = \sqrt{16 + 9} = \sqrt{25} = 5 \\[1 em] \| \vec{b} \| &= \sqrt{(-2)^2 + 2^2} = \sqrt{4 + 4} = \sqrt{8} \end{aligned} $$Now we'll find the $ \cos \alpha $
$$ \cos \alpha = \dfrac{\vec{a} \cdot \vec{b}}{ \|\vec{a}\| \, \|\vec{b}\|} = \dfrac{-2}{5 \sqrt{8}} \approx -0.1414 $$The angle $ \alpha $ is:
$$ \alpha = \cos^{-1}(-0.1414) \approx 98^{o} $$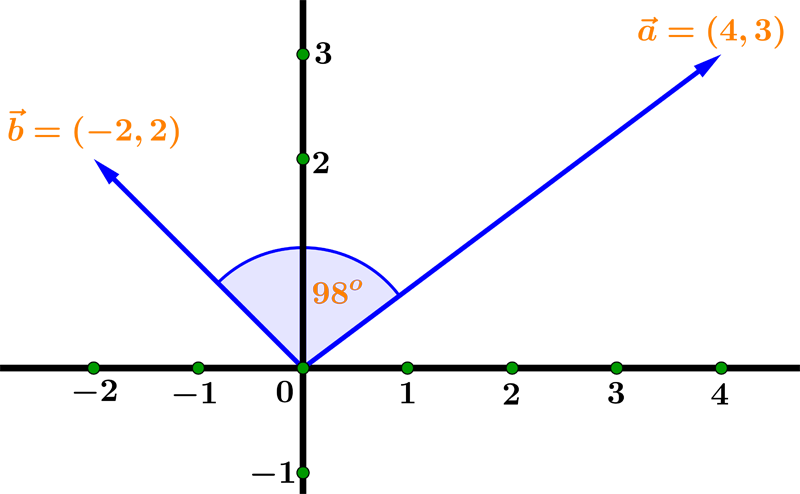
Example 06: Find the angle between vectors $ \vec{v_1} = \left(2, 1, -4 \right) $ and $ \vec{v_2} = \left( 3, -5, 2 \right) $.
4 : Cross product
The cross product of vectors $ \vec{v} = (v_1,v_2,v_3) $ and $ \vec{w} = (w_1,w_2,w_3) $ is given by the formula:
$$ \vec{v} \times \vec{w} = \left( v_2 w_3 - v_3 w_2, v_3 w_1 - v_1 w_3, v_1 w_2 - v_2 w_1 \right) $$Note that the cross product requires both of the vectors to be in three dimensions.
If the two vectors are parallel than the cross product is equal zero.
Example 07: Find the cross products of the vectors $ \vec{v} = ( -2, 3 , 1) $ and $ \vec{w} = (4, -6, -2) $. Check if the vectors are parallel.
We'll find cross product using above formula
$$ \begin{aligned} \vec{v} \times \vec{w} &= \left( 3 \cdot (-2) - 1 \cdot (-6), 1 \cdot 4 - (-2) \cdot (-2), -2 \cdot (-6) - 3 \cdot 4 \right) = \\[1 em] &= \left(-6-(-6), 4-4,12 - 12 \right) = (0, 0, 0) \end{aligned} $$Since the cross product is zero we conclude that the vectors are parallel.
Example 08: Find the cross products of the vectors $ \vec{v_1} = \left(4, 2, -\dfrac{3}{2} \right) $ and $ \vec{v_2} = \left(\dfrac{1}{2}, 0, 2 \right) $.
Please tell me how can I make this better.