- Calculators
- ::
- Numbers
- ::
- Scientific notation calculator
Scientific notation calculator
This scientific notation converter/calculator makes a conversion between scientific and decimal notation, and performs arithmetic operations on scientific numbers. The calculator can multiply, divide, and evaluate powers of numbers written in scientific notation.
error
This field is required

Scientific Notation
Scientific notation is a way of writing very large or very small numbers. In scientific notation, every number is represented as a × 10n, where the decimal number a is greater than 1 and lesser than 10. We will provide some examples of how to convert numbers to scientific notation.
Convert 7823.5 to scientific notation
In this example, we need to convert a number, which is greater than 10. To do so move decimal point to the left until you get number lesser than 10. Because the decimal is moved three places, we conclude that n = 3.
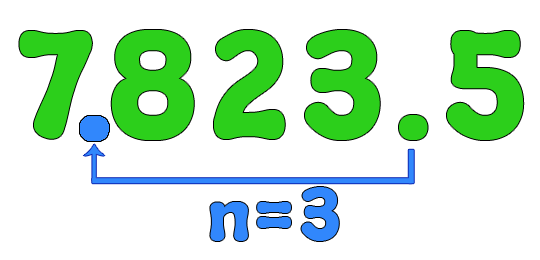
The result is:
$$ 7823.5 = 7.8235 \times 10^{\color{blue}{3}} $$Convert 7800000 to scientific notation
In this example, there is no decimal point at the end of the number, so we will add one. Now, move the decimal point between the digits 7 and 8. Since the decimal is moved six places, we can conclude that n = 6.
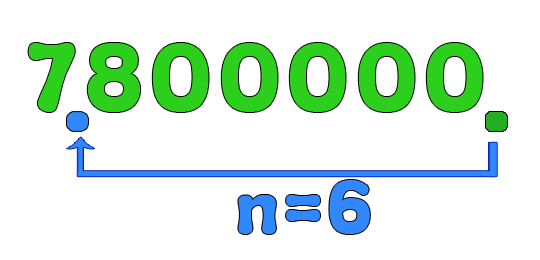
The result is:
$$ 7800000 = 7.8 \times 10^{\color{blue}{6}} $$Convert 0.00000254 to scientific notation
To convert the small number to scientific notation, move the decimal point to the right (between digits 2 and 5). Since the decimal was moved 8 spaces to the right, we might conclude that the n is -8.
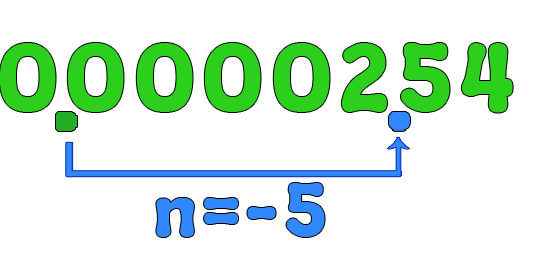
The result is:
$$ 0.0000000254 = 2.54 \times 10^{\color{blue}{-8}} $$Multiply $1.2 \cdot 10^5 $ by $3.45 \cdot 10^-8$
To multiply numbers written in scientific notation we first multiplay numeric parts,
1.2 * 3.45 = 4.14
After that, we multiply powers of 10.
105 * 10-8 = 105-8 = 10-3
Putting everything together, we get:
$$ 1.2\cdot 10^5 \cdot 3.45 \cdot 10^{-8} = 4.14 10^{-3} $$1. Writing Large and Small Numbers - with examples and solutions
2. Scientific Notation of Small Numbers
3. Multiplication and Division - video tutorial