- Calculators
- ::
- Analytic Geometry
- ::
- Two point form
Two point form calculator
This online calculator finds and plots the equation of a straight line passing through the two given points. The calculator generates a step-by-step explanation of how to get the result.
Find the equation of the line passing through the points: $$ A=\left(0,~0\right) \text{ and }B=\left(100,~100\right) $$
solution
The equation of the line passing through point $ A=\left(0,~0\right) $, and point $ B=\left(100,~100\right) $ is:
$$ y = x $$explanation
To find equation of the line passing through points $ A(x_A,y_A) $ and $ B(x_B,y_B) $, we use formula:
$$ y - y_A~=~\frac{y_B - y_A}{x_B - x_A}(x-x_A) $$In this example we have:
$$ \begin{aligned} & A=\left(0,~0\right) \implies x_A = 0 ~~\text{and}~~ y_A = 0 \\[1 em] & B=\left(100,~100\right) \implies x_B = 100 ~~\text{and}~~ y_B = 100 \end{aligned} $$After substituting into the formula, we obtain:
$$ \begin{aligned} y - y_A~&=~\frac{y_B - y_A}{x_B - x_A}(x - x_A) \\[1 em] y - 0~&=~\frac{ 100 - 0 }{ 100 - 0 } \left( x - 0 \right) \\[1 em]y - 0 ~&=~ 1 \left( x - 0 \right) \\[1 em]y - 0 ~&=~ 1x + 0 \\[1 em]y ~&=~ 1x + 0 \end{aligned} $$How to find equation of the line determined by two points?
To find equation of the line passing through points $A(x_A, y_A)$ and $B(x_B, y_B)$ ( $ x_A \ne x_B $ ), we use formula:
$$ {\color{blue}{ y - y_A = \frac{y_B - y_A}{x_B-x_A}(x-x_A) }} $$Example:
Find the equation of the line determined by $A(-2, 4)$ and $B(3, -2)$.
Solution:
In this example we have: $ x_A = -2,~~ y_A = 4,~~ x_B = 3,~~ y_B = -2$. So we have:
$$ \begin{aligned} y - y_A & = \frac{y_B - y_A}{x_B-x_A}(x-x_A) \\ y - 4 & = \frac{-2 - 4}{3 - (-2)}(x - (-2)) \\ y - 4 & = \frac{-6}{5}(x + 2) \end{aligned} $$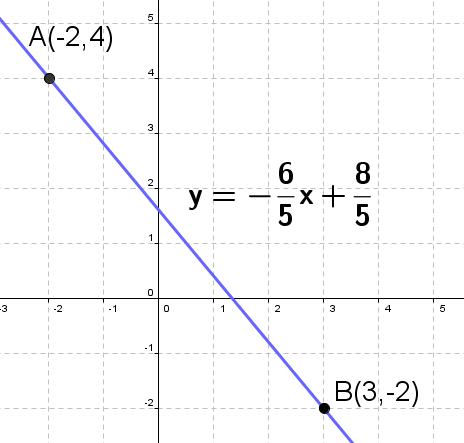
Multiply both sides with $5$ to get rid of the fractions.
$$ \begin{aligned} (y - 4)\cdot {\color{red}{ 5 }} & = \frac{-6}{5}\cdot {\color{red}{ 5 }}(x + 2)\\ 5y - 20 & = -6(x + 2)\\ 5y - 20 & = -6x - 12 \\ 5y & = -6x - 12 + 20 \\ 5y & = -6x + 8 \\ {\color{blue}{ y }} & {\color{blue}{ = -\frac{6}{5}x - \frac{8}{5} }} \end{aligned} $$In special case (when $x_A = x_B$ the equation of the line is:
$$ {\color{blue}{ x = x_A }} $$Example 2:
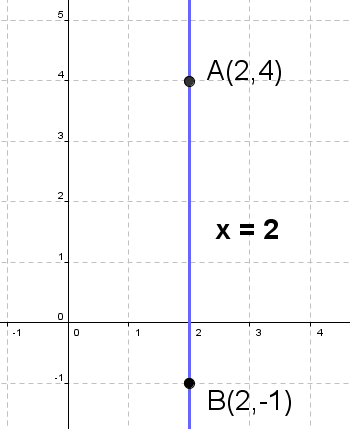
Find the equation of the line determined by $A(2, 4)$ and $B(2, -1)$.
Solution:
In this example we have: $ x_A = 2,~~ y_A = 4,$ $ x_B = 2,~~ y_B = -1$. Since $x_A = x_B$, the equation of the line is:
$$ {\color{blue}{ x = 2 }} $$You can see from picture on the right that in special case the line is parallel to y - axis.
Note: use above calculator to check the results.
Please tell me how can I make this better.