Division of Polynomials »

Before starting to multiply polynomials, make sure you are familiar with the sections on adding and subtracting polynomials and exponents. We are going to examine the rules for multiplying one polynomial by another polynomial.

Multiplying a Monomial by a Polynomial

We start with an examination of how to multiply (or distribute) a monomial by a polynomial:

Example 1:

Perform the following multiplication: $3{x^2} = (4x + 6)$

Solution:

Just like when you multiply a number in front of the brackets through the brackets (distribute) you must multiply the monomial in front of the brackets through the brackets, as shown below:

Remember when multiplying terms to multiply the coefficients first, then the variable parts. So:

$3{x^2}(4x) = 12{x^3}$ and $3{x^2}(6) = 18{x^2}$

Therefore, your final expression is:

$12{x^3} + 18{x^2}$

Multiplying a Polynomial by a Polynomial

The process of multiplication gets harder when you are multiplying two polynomials of two or more terms together. The rule to remember is:

Multiply EVERY term of the first polynomial by EVERY term of the second polynomial.

We will try to illustrate this with a couple of examples:

Example 2:

Perform the following multiplication:

$(x + 6)(x - 3)$

Solution

Here we have two polynomials: (x + 6) and (x - 3) that are being multiplied together. Looking back at the rule for this situation (multiply EVERY term of the first polynomial by EVERY term of the second polynomial) helps us organize what we have to do. We must multiply the first x in the first polynomial by the x AND the -3 in the second polynomial. We must also multiply the 6 in the first polynomial by the x and the -3 in the second polynomial. In pictorial form, this looks like:

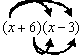
So there are four multiplications that need to be calculated: x(x) = x², x(-3) = -3x, 6(x) = 6x and 6(-3) = -18. List these results as a new expression:

${x^2} - 3x + 6x - 18$

The last step is to ensure that if there are any like terms that you combine them. The -3x and the 6x are like terms in the above expression, so they must be combined. This leaves you with the following expression, which is the final answer:

${x^2} + 3x - 18$

Example 3:

Perform the following multiplication:

$(2a + 3b - 7)({a^3} - 2{a^2} + 2a + 1)$

Solution:

Working through a long example like this can be confusing. The key is to take your time and perform each step carefully. The rule for multiplication is so important it is stated again here:

Multiply EVERY term of the first polynomial by EVERY term of the second polynomial.

Essentially we need to perform three long multiplications: the 2a in the first polynomial by every term in the second polynomial, the 3b in the first polynomial by every term in the second polynomial and the -7 in the first polynomial by every term in the second polynomial. One way to organize all of this multiplication is to write them out separately, as shown below:

$$2a({a^3} - 2{a^2} + 2a + 1) = 2{a^4} - 4{a^3} + 4{a^2} + 2a$$ and... $$3b({a^3} - 2{a^2} + 2a + 1) = 3{a^3}b - 6{a^2}b + 6ab + 3b$$ and... $$- 7({a^3} - 2{a^2} + 2a + 1) = - 7{a^3} + 14{a^2} - 14a - 7$$

Now put the right hand side of all of these multiplications together on one line to get:

$2{a^4} - 4{a^3} + 4{a^2} + 2a + 3{a^3}b - 6{a^2}b + 6ab + 3b - 7{a^3} + 14{a^2} - 14a - 7$

You're not quite done yet!!! Remember, you must find and combine any like terms. Once this is done, you end up with your final expression:

$2{a^4} - 11{a^3} + 18{a^2} - 12a + 3{a^3}b - 6{a^2}b + 6ab + 3b - 7$