Volume »

The area between the curves $y = f(x)$ and $y = g(x)$ between $x = a$ and $x = b \ \ (a < b)$ is given by

$$A = \int\limits_a^b {\left| {f(x) - g(x)} \right|dx}$$

Example 1:

Find the area of the region bounded by the graphs of $f(x) = 2 - x^2$ and $g(x) = x$

Solutions:

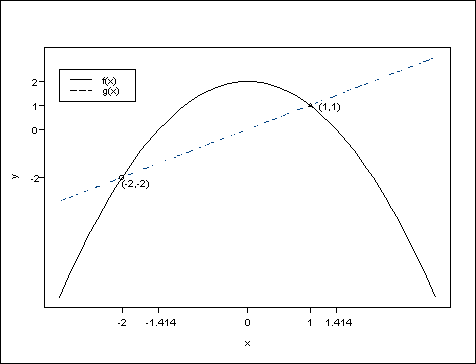
The two lines intersect at the points $(-2, -2)$ and $(1, 1)$ since

$$f(x) = g(x) \leftrightarrow 2 - x^2 = x \leftrightarrow x^2 + x - 2 = 0 \leftrightarrow x = -2 , 1$$

Thus, the area is

$$\begin{aligned} A &= \int\limits_a^b {\left| {f(x) - g(x)} \right|dx = \int\limits_{ - 2}^1 {\left| {2 - {x^2} - x} \right|dx} } = \int\limits_{ - 2}^1 {(2 - {x^2} - x)dx} = \\ &= \left[ { - \frac{x^3}{3} - \frac{x^2}{2} + 2x} \right]_{ - 2}^1 = \\ &= \frac{9}{2} \end{aligned}$$

Example 2:

Find the area of the region bounded by the graphs of $f(x) = 3x^3 - x^2 - 10x$ and $g(x) = -x^2 + 2x$

Solution:

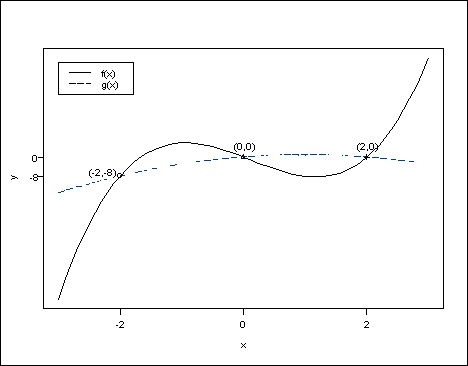
The two lines intersect at the points $( -2, -8)$, $( 0, 0)$ and $( 2, 0)$ since

$$f(x) = g(x) \leftrightarrow 3x^3 - x^2 - 10x = -x^2 + 2x \leftrightarrow 3x^3 - 12x = 0 \leftrightarrow x = -2, 0, 2$$.

Thus, the area is

$$\begin{aligned} A &= \int\limits_{ - 2}^2 {\left| {f(x) - g(x)} \right|dx = \int\limits_{ - 2}^0 {\left[ {f(x) - g(x)} \right]dx} } + \int\limits_0^2 {\left[ {g(x) - f(x)} \right]dx} = \\ &= \int\limits_{ - 2}^0 {\left[ {3{x^3} - {x^2} - 10x - ( - {x^2} + 2x)} \right]dx} + \int\limits_0^2 {\left[ {( - {x^2} + 2x) - (3{x^3} - {x^2} - 10x)} \right]dx} = \\ &= \int\limits_{ - 2}^0 {(3{x^3} - 12x)dx} + \int\limits_0^2 {( - 3{x^3} + 12x)dx} = \\ &= \left[ {\frac{{3{x^4}}}{4} - 6{x^2}} \right]_{ - 2}^0 + \left[ {\frac{{ - 3{x^4}}}{4} + 6{x^2}} \right]_0^2 = - (12 - 24) + ( - 12 + 24) = 24 \end{aligned}$$