Ellipse »

Definition:

The General Form of the Circle

An equation, written in the following form, represents a circle except when
$D^2 + E^2 \le F$

This is called the general form of the circle .

$C(-D, -E)$ is the center of the circle, and the radius is $r = \sqrt{D^2 + E^2 - F}$

Example 1:

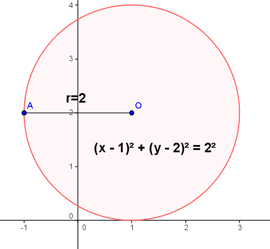
Find the radius and center of the circle $x^2 + y^2 - 2x - 4y + 1 = 0$

Solution:

It is needed to get the equation into the form: $(x - a)^2 + (y - b)^2 = r^2$

$$\begin{aligned} &x^2 + y^2 - 2x - 4y + 1 = 0 \\ &x^2 - 2x + y^2 - 4y = -1 \\ &x^2 - 2x + 1 + y^2 - 4y \color{red}{+ 4} = -1 \color{blue}{+ 1} \color{red}{+ 4} \\ &\color{blue}{(x - 1)^2} + \color{red}{(y - 2)^2} = 2^2 \end{aligned}$$

The radius of circle is $r = 2$ and the center of the circle is $O(1, 2)$.

In this example $D = -1$, $E = 2$, $F = 1$

Equation of a Circle from 3 Points

Example 2:

Find the equation of the circle through the points $A(4, -2)$, $B(6, 1)$, $C(-1, 3)$.

Let $x^2 + y^2 + 2Dx + 2Ex + F = 0$ represent the circle. Since $A$ is on the circle, its coordinates, 4 and -2, satisfy the equation

Whence: $8D - 4E + F = -20$.

Similarly, for $B$, $12D + 2E + F = -37$.

and for $C$, $-2D + 6E + F = -10$.

Solving this, gotten values are: $D = - \frac{23}{10}$, $E = - \frac{13}{10}$, $F = -\frac{34}{5}$, and the equation is: $x^2 + y^2 - \frac{23}{5} x - \frac{13}{5} y - \frac{34}{5} = 0$

Equation of a tangent at a given point

Let $A(x_1, y_1)$ be a point of the circle $(x - a)^2 + (y - b)^2 = r^2 , then an equation of tangent line to circle is:

Example:

Given the circle $(x - 1)^2 + (y - 2)^2 = 25$ and the point $A(4,6)$ on the circle, find the equation of the tangent to the circle at $A$.

Solution:

Here we have: $a = 1$, $b = 2$, $x_1 = 4$, $y_1 = 6$

The equation of tangent is:

$$\begin{aligned} (x_1 - a) (x - a) + (y_1 - b) (y - b) &= f^2 \\ (4 - 1) (x - 1) + (6 - 2) (y - 2) &= 5^2 \\ 3 (x - 1) + 4 (y - 2) &= 25 \\ 3x + 4y - 3 - 8 - 25 &= 0 \\ \color{blue}{3x + 4y - 36} &\color{blue}{= 0} \end{aligned}$$