- Math Lessons
- >
- Linear Algebra
- >
- Vectors
- >
- Cross Product
| « Dot Product |
|
Cross Product
Besides the usual addition of vectors and multiplication of vectors by scalars, there are also two types of multiplication of vectors by other vectors. One type, the dot product, is a scalar product; the result of the dot product of two vectors is a scalar. The other type, called the cross product, is a vector product since it yields another vector rather than a scalar. As with the dot product, the cross product of two vectors contains valuable information about the two vectors themselves.
The cross product of two vectors
and
is given by
Although this may seem like a strange definition, its useful properties will soon become evident. There is an easy way to remember the formula for the cross product by using the properties of determinants. Recall that the determinant of a 2x2 matrix is
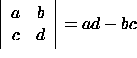
and the determinant of a 3x3 matrix is
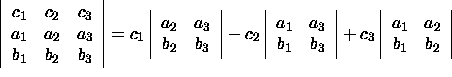
Notice that we may now write the formula for the cross product as
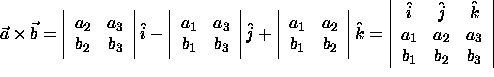
Example 1:
The cross product of the vectors
and
.
Solution:
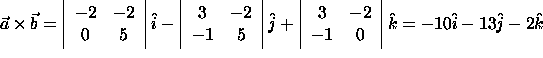
Properties of the Cross Product:
1. The length of the cross product of two vectors is
2. Anticommutativity:
3. Multiplication by scalars:
4. Distributivity:
5. The scalar triple product of the vectors a, b, and c:
Example 2
Calculate the area of the parallelogram spanned by the vectors a = <3, - 3, 1> and b = <4, 9, 2>.
Solution:
The area is
. Using
the above expression for the cross product, we find that the area is
