Math formulas: Solutions of algebraic equations

0 formulas included in custom cheat sheet

Quadric Equation: $ax^2 + bx + c = 0 $

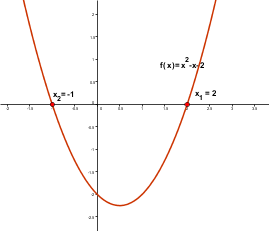
Solutions (roots):

$$ x_{1,2} = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} $$

If $ D = b^2 - 4ac $ is the discriminant , then the roots are

1. real and unique if $ D > 0 $

2. real and equal if $ D = 0 $

3. complex conjugate if $ D < 0 $

Cubic Equation: $x^3 + a_1x^2 + a_2x + a_3 = 0 $

Let

$$ \begin{aligned} Q &= \frac{3a_2 - a_1^2}{9} \\ R &= \frac{9a_1a_2 - 27a_3 - 2a_1^3}{54} \\ S &= \sqrt[\Large3]{R + \sqrt{Q^3 + R^2}} \\ T &= \sqrt[\Large3]{R - \sqrt{Q^3 + R^2}} \end{aligned} $$

Then solutions (roots) of the cubic equation are:

$$ \begin{aligned} x_1 &= S + T - \frac{1}{3}a_1 \\ x_2 &= -\frac{1}{2} (S + T) - \frac{1}{3}a_1 + \frac{1}{2}\,i\,\sqrt{3}(S-T) \\ x_3 &= -\frac{1}{2} (S + T) - \frac{1}{3}a_1 - \frac{1}{2}\,i\,\sqrt{3}(S-T) \end{aligned} $$

If $D = Q^3 + R^2 $ is the discriminant of the cubic equation, then:

1. one root is real and two complex conjugate if $D > 0$

2. all roots are real and at last two are equal if $D=0$

3. all roots are real and unequal if $D < 0$

Quartic Equation:$x^4 + a_1x^3 + a_2x^2 + a_3x + a_4 = 0 $

Let $y_1$ be a real root of the cubic equation

$$ y^3 - a_2y^2 + (a_1a_3-4a_4)y+(4a_2a_4 - a_3^2 - a_1^2a_4) = 0 $$

Then solutions of the quartic equation are the 4 roots of

$$ z^2 + \frac{1}{2}\left(a_1 \pm \sqrt{a_1^2 - 4a_2+4y_1}\right)z + \frac{1}{2}\left(y_1 \pm \sqrt{y_1^2 - 4a_4}\right)= 0 $$