Rhombus calculator
This calculator finds the unknown element of a rhombus given any two known dimensions. The calculator can determine side, area, long and short diagonal, perimeter, height, incircle radius, and interior angle. The calculator gives you a step-by-step solution on how to find the missing value.
Find the side $ a $ of a rhombus if diagonal $d_2 = 59\, \text{cm}$ and angle $\beta = 59^o$.
solution
$$ a \approx 56.4094\, \text{cm} $$explanation
STEP 1: find angle $ \alpha $
To find angle $ \alpha $ use formula:
$$ \alpha + \beta = 90^o $$After substituting $ \beta = 59^o $ we have:
$$ \alpha + 59^o = 90^o $$ $$ \alpha = 90^o - 59^o $$ $$ \alpha = 31^o $$STEP 2: find height $ h $
To find height $ h $ use formula:
$$ \sin \left( \frac{ \beta }{ 2 } \right) = \dfrac{ h }{ d_2 } $$After substituting $\beta = 59^o$ and $d_2 = 59\, \text{cm}$ we have:
$$ \sin \left( \frac{ 59^o }{ 2 } \right) = \dfrac{ h }{ d_2 } $$ $$ \sin( \frac{ 59 }{ 2 }^o ) = \dfrac{ h }{ 59 } $$ $$ 0.4924 = \dfrac{ h }{ 59 } $$$$ h = 0.4924 \cdot 59 $$$$ h = 29.053 $$STEP 3: find side $ a $
To find side $ a $ use formula:
$$ \sin \left( \alpha \right) = \dfrac{ h }{ a } $$After substituting $\alpha = 31^o$ and $h = 29.053\, \text{cm}$ we have:
$$ \sin( 31^o ) = \dfrac{ 29.053\, \text{cm} }{ a } $$ $$ 0.515 = \dfrac{ 29.053\, \text{cm} }{ a } $$ $$ a = \dfrac{ 29.053\, \text{cm} }{ 0.515 } $$ $$ a = 56.4094\, \text{cm} $$Tutorial
What is a rhombus?
A rhombus is a quadrilateral with four equal sides. Consequently, the opposite sides of a rhombus are parallel. The square is a special case of a rhombus with all angles equal to 90 degrees.
Rhombus attributes
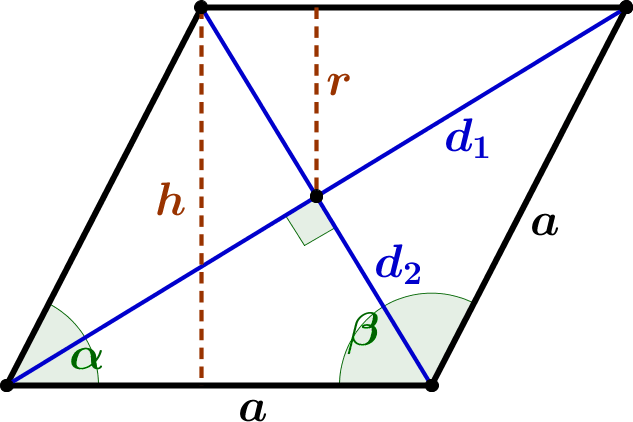
The most important formulas?
The calculator uses the following formulas to find the missing elements of a rhombus.
1. Area – version 1
A = d1 d2 /2
2. Area – version 2
A = ah
3. Area – version 3
A = a2 sin(α)
4. Perimeter
P = 4a
5. Height
h = a × sin(α)
6. Sum of angles
α + β = 1o
7. Side of a rhombus
a2 = d12/4 + d22/4
8. Long diagonal
d12 = 2a2(1 - cos(α))
9. Short diagonal
d22 = 2a2(1 - cos(β))
Solved examples
Example 1:
Find the area of a rhombus if the diagonals are d1=16cm and d2=7cm.
A = (d1 · d2)/2
A = (16·7)/2
A = 8·7
A = 56
Example 2:
Calculate the height of a rhombus with if the longer diagonal is d1=16cm and the side is a=10cm.
Step 1: Find second diagonal:
a2 = d12/4 + d22/4
102 = 162/4 + d22/4
100 = 256/4 + d22/4
d22/4 = 100 - 64
d22/4 = 36
d22 = 144
d2 = 12
Step 2: Find the area:
A = (d1·d2)/2
A = (16·12)/2
A = 192/2
A = 96
Step 3: Find the height of a rhombus:
A = a·h
96 = 10·h
h = 96/10
h = 9.6
1. Area of a rhombus — worked examples