- Math Lessons
- >
- Linear Algebra
- >
- Vectors
- >
- Dot Product
| « Basic Operations with Vectors |
Dot Product
Definition:
The dot product (also called the inner product or scalar product) of two vectors is defined as:
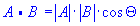
Where |A| and |B| represents the magnitudes
of vectors A and B and 
is the angle between vectors A
and B.
Dot product calculation
The dot or scalar product of vectors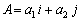 
and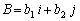 
can be written as:
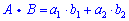
Example (calculation in two dimensions):
Vectors A and B are given by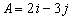 
and
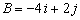. Find the dot product
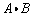of the two vectors.
Solution:
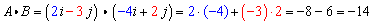
Example (calculation in three dimensions):
Vectors A and B are given by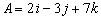 
and
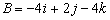. Find the dot product
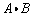of the two vectors.
Solution:
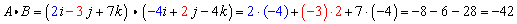
Calculating the Length of a Vector
The length of a vector 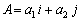is:
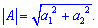
Example:
Vector A is given by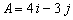 
.
Find |A|.
Solution:
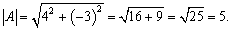
The angle between two vectors
The angle between two nonzero vectors A and B is
Example: (angle between vectors in two dimensions):
Determine the angle between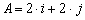 
and
.
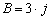Solution:
We will need the magnitudes of each vector as well as the dot product.
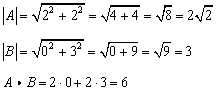
The angle is,
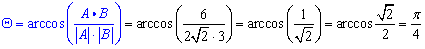
Example: (angle between vectors in three dimensions):
Determine the angle between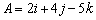 
and
.
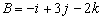Solution:
Again, we need the magnitudes as well as the dot product.
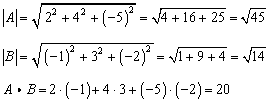
The angle is,
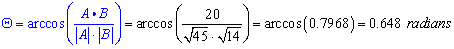
Orthogonal vectors
If two vectors are orthogonal then:
.
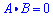Example:
Determine if the following vectors are orthogonal:
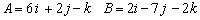
Solution:
The dot product is
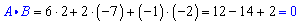
So, the two vectors are orthogonal.