- Math Lessons
- >
- Algebra
- >
- Solving System of Linear Equations
- >
- Row Reduction Method
| « Elimination Method |
Row Reduction Method
The principles involved in row reduction of matrices are equivalent to those we used in the elimination method of solving systems of equations. That is, we are allowed to
1. Multiply a row by a non-zero constant.
2. Add one row to another.
3. Interchange between rows
4. Add a multiple of one row to another.
How do we use this to solve systems of equations? We follow the steps:
Step 1. Write the augmented matrix of the system.
Step 2. Row reduce the augmented matrix.
Step 3. Write the new, equivalent, system that is defined by the new, row reduced, matrix.
Step 4. Solution is found by going from the bottom equation
Example: solve the system of equations using the row reduction method
$$ \begin{aligned} 3x + 2y - z &= 1\\ x - 2y + z &= 0\\ 2x + y - 3z &= -1 \end{aligned} $$Solution:
Step 1: Write the augmented matrix of the system:
$$ \left[ {\begin{array}{*{20}{c}} 3\\ 1\\ 2 \end{array}\begin{array}{*{20}{c}} 2\\ 2\\ 1 \end{array}\begin{array}{*{20}{c}} { - 1}\\ 2\\ 3 \end{array}\begin{array}{*{20}{c}} 1\\ 0\\ { - 1} \end{array}} \right] $$Step 2: Row reduce the augmented matrix:
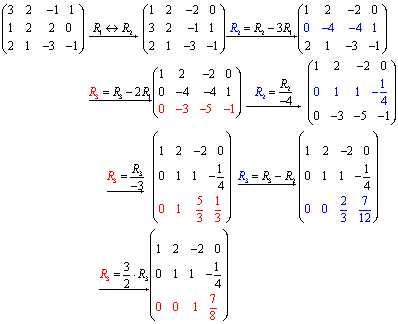
The symbols we used above the arrows are short for:
R1 <--> R2 Interchange Rows 1 and 2.
R2 = R2 - 3R2 New Row2 = old Row2 minus 3 times Row1
R2 = R2/-4 Divide Row 2 by -4.
Step 3:
Rewrite the system using the row reduced matrix:
$$ \begin{aligned} x + 2y + (-2)z &= 0\\ y + z &= - \frac{1}{4}\\ z &= \frac{7}{8} \end{aligned} $$Step 4:
And the solution is found by going from the bottom equation up:
$$ \begin{aligned} z &= \frac{7}{8}\\ y &= - \frac{1}{4} - z = - \frac{1}{4} - - \frac{7}{8} = - \frac{9}{8}\\ x &= 0 + 2z - 2y = 2\cdot \frac{7}{8} - 2 \cdot \left( { - \frac{9}{8}} \right) = 4 \end{aligned} $$