« Complex number arithmetic

Polar representation of complex numbers

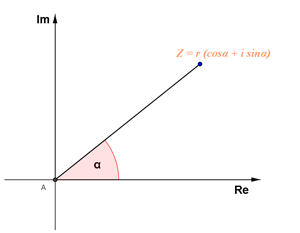
In polar representation a complex number z is represented by two parameters r and Θ. Parameter r is the modulus of complex number and parameter Θ is the angle with the positive direction of x-axis.

This representation is very useful when we multiply or divide complex numbers.

Polar to Rectangular Form Conversion

Here we know r and Θ and we need to find a and b.

Example 1:

Convert the complex number $z = 4(\cos {60^ \circ } - i\sin {60^ \circ })$ to rectangular form.

Solution:

$z = 4(\cos {60^ \circ } - i\sin {60^ \circ }) = 4\left( {\frac{1}{2} - i\frac{{\sqrt 3 }}{2}} \right) = 2 - 2\sqrt {3i}$

Exercise 1: Convert to rectangular form:

Rectangular to Polar Form Conversion

Here we know a and b and we need to find r and Θ. In this case we need to use formulas:

$$r = \sqrt {{a^2} + {b^2}} $$ $$tg\theta = \frac{b}{a}$$

Example 2:

Convert the complex number $z = 2 - 2\sqrt {3i} $ to polar form.

Solution:

In this example $a = 2$ $b = - 2\sqrt 3 $:

$$r = \sqrt {{a^2} + {b^2}} = \sqrt {{2^2} + {{( - 2\sqrt 3 )}^2}} = \sqrt {4 + 12} = 4$$ $$tg\theta = \frac{b}{a} = \frac{{ - 2\sqrt 3 }}{2} = - \sqrt 3 \Rightarrow \theta = - {60^ \circ }$$

The polar form is:

$z = 4(\cos ( - {60^ \circ }) + i\sin ( - {60^ \circ })) = 4(\cos {60^ \circ } - i\sin {60^ \circ })$

Exercise 2: Convert to polar form:

Product in polar representation

$r(\cos \theta - i\sin \theta ) \cdot r(\cos {\theta ^t} - i\sin {\theta ^t}) = r \cdot {r^t}(\cos (\theta + {\theta ^t}) + i\sin (\theta + {\theta ^t}))$

Example 3:

Let ${z_1} = 2(\cos {30^ \circ } + i\sin {30^ \circ })$, ${z_2} = 3(\cos {120^ \circ } + i\sin {120^ \circ })$. Then:

${z_1} \cdot {z_2} = 2 \cdot 3(\cos ({30^ \circ } + {120^ \circ }) + i\sin ({30^ \circ } + {120^ \circ })) = 6(\cos {150^ \circ } + i\sin {150^ \circ })$

Quotient two complex numbers in polar representation

$\frac{{r(\cos \tau + i\sin \tau )}}{{{r^t}(\cos \theta + i\sin \theta )}} = \frac{r}{{{r^t}}}(\cos (\tau - \theta ) + i\sin (\tau - \theta ))$

Example 4:

Let ${z_1} = 2(\cos {30^ \circ } + i\sin {30^ \circ })$, ${z_2} = 3(\cos {120^ \circ } + i\sin {120^ \circ })$. Then:

$$\frac{{{z_1}}}{{{z_2}}} = \frac{2}{3}(\cos ({30^ \circ } - {120^ \circ }) + i\sin ({30^ \circ } - {120^ \circ })) = $$ $$ = \frac{2}{3}(\cos ( - {90^ \circ }) + i\sin ( - {90^ \circ })) = $$ $$ = \frac{2}{3}(\cos {90^ \circ } - i\sin {90^ \circ })$$

Exercise 3: Find product and quotient:

The inverse of a complex number in polar representation

$\frac{1}{{r(\cos \theta + i\sin \theta )}} = \frac{1}{r}(\cos \theta - i\sin \theta )$

Conjugate numbers in polar representation

$\overline {r(\cos \theta + i\sin \theta )} = r(\cos \theta - i\sin \theta )$

Formula 'De Moivre'

${(\cos \theta + i\sin \theta )^n} = \cos (n\theta ) + i\sin (n\theta )$

Example 5:

Let z = 1 - i.

a) find polar representation

b) find z⁸

Solution:

a) $z = \sqrt 2 (\cos {45^ \circ } + i\sin {45^ \circ })$

b) ${z^8} = {\left[ {\sqrt 2 (\cos {{45}^ \circ } + i\sin {{45}^ \circ })} \right]^8} = {\sqrt 2 ^8} \cdot {(\cos {45^ \circ } + i\sin {45^ \circ })^8} = {2^4} \cdot (\cos (8 \cdot {45^ \circ }) + i\sin (8 \cdot {45^ \circ })) = 16(\cos {360^ \circ } + isin{360^ \circ }) = 16(1 + i \cdot 0) = 16$

Exercise 4: Find zⁿ: