« Circle

Hyperbola »

Definitions:

1. An ellipse is the figure consisting of all those points for which the sum of their distances to two fixed points (called the foci) is a constant.

2. An ellipse is the figure consisting of all points in the plane whose Cartesian coordinates satisfy the equation

$\frac{(x - h)^2}{a^2} + \frac{(y - k)^2}{b^2} = 1$

Where $h$, $k$, $a$ and $b$ are real numbers, and $a$ and $b$ are positive.

Formulas:

Equations

An ellipse centered at the point $(h, k)$ and having its major axis parallel to the x-axis is specified by the equation

$\frac{(x - h)^2}{a^2} + \frac{(y - k)^2}{b^2} = 1$

Parametric equations of the ellipse:

$$\begin{aligned} &x = h + a \cos t \\ &y = k + b \cos t \\ &-\pi \le t < \pi \end{aligned}$$

Major axis = 2a

Minor axis = 2b

Eccentricity

Define a new constant $0 \le \varepsilon < 1$ called the eccentricity ( $\varepsilon = 0$ is the case of a circle) The eccentricity is:

$\varepsilon = \sqrt{1 - \frac{b^2}{a^2}}$.

The greater the eccentricity is, the more elongated is the ellipse.

Foci:

If $c$ equals the distance from the center to either focus, then

$$\begin{aligned} &F1: \ \ \left( h - \sqrt{a^2 - b^2}, \ \ k \right) \\ &F2: \ \ \left( h + \sqrt{a^2 - b^2}, \ \ k \right) \end{aligned}$$

The distance between the foci is $2 a \varepsilon$.

Area

The area enclosed by an ellipse is $\pi a b$, where, in the case of a circle where $a = b$, the expression reduces to the familiar $a^2 \pi$

Tangent line

If $D(x_0, y_0)$ is a fixed point of the ellipse.

The equation of the tangent line in point $D(x_0, y_0)$ of an ellipse

$\frac{x_0 (h - x)}{a^2} + \frac{y_0 (k - y)}{b^2} = 1$

Example 1:

Given the following equation

$9x^2 + 4y^2 = 36$

Find the length of the major and minor axes.

b) Find the coordinates of the foci.

c) Sketch the graph of the equation.

Solution:

a) First write the given equation in standard form:

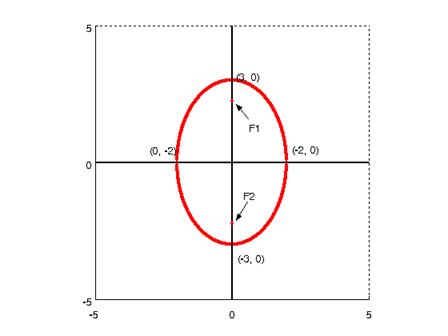
$$\begin{aligned} 9x^2 + 4y^2 &= 36 \ \ / \color{blue}{36} \\ \frac{9x^2}{36} + \frac{4y^2}{36} &= 1 \\ \frac{x^2}{4} + \frac{y^2}{9} &= 1 \\ \frac{x^2}{2^2} + \frac{y^2}{3^2} &= 1 \ \ \to \ \ \color{blue}{a = 2; \ b = 3} \end{aligned}$$

The major axis length is given by $= 2a = 4$

The minor axis length is given by $= 2b = 6$

b)

$$\begin{aligned} &F1: \ \ \left( h, k - \sqrt{b^2 - a^2} \right) = \left( 0,0 - \sqrt{3^2 - 2^2} \right) = \color{blue}{\left( 0, - \sqrt{5} \right)} \\ &F2: \ \ \left( h, k + \sqrt{b^2 - a^2} \right) = \left( 0,0 + \sqrt{3^2 - 2^2} \right) = \color{blue}{\left( 0, \sqrt{5} \right)} \end{aligned}$$

c)

Example 2:

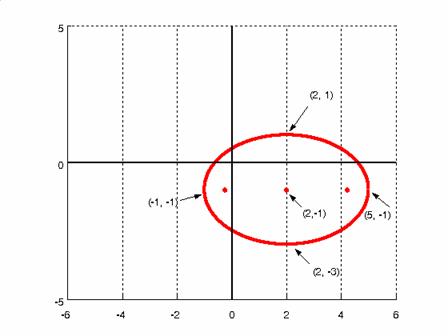
Sketch the graph of the ellipse whose equation is $\frac{(x - 2)^2}{9} + \frac{(y + 1)^2}{4} = 1$.

Solution:

It can be seen that the center of the ellipse is $(h, k) = (2, -1)$. Next, note that $a = 3, b = 2$.

It is known that the endpoints of the major axis are exactly 3 units left and right from the center, which places them at the points $(-1, -1)$ and $(5, -1)$.

It is, also, known that the endpoints of the minor axis are exactly 2 units above and below the center, which places them at the points $(2, 1)$ and $(2, -3)$.

Foci:

$$\begin{aligned} &F1: \ \ \left( h - \sqrt{a^2 - b^2}, k \right) = \left( 2 - \sqrt{3^2 - 2^2}, -1 \right) = \left( 2 - \sqrt{5}, -1 \right) \\ &F1: \ \ \left( h + \sqrt{a^2 - b^2}, k \right) = \left( 2 + \sqrt{3^2 - 2^2}, -1 \right) = \left( 2 + \sqrt{5}, -1 \right) \end{aligned}$$