Compound interest calculator

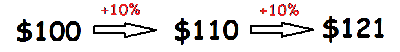
problem

Suppose that a savings account is compounded yearly with a principal of $1700. After 2 years years, the amount increased to $1910. What was the per annum interest rate?

solution

Interest rate per anum was 6%.

explanation

To find interest rate we use formula:

$$ A = P \left( 1 + \frac{r}{n} \right)^{\Large{n \cdot t}} $$

A = total amount P = principal (amount of money deposited) r = annual interest rate n = number of times compounded per year t = time in years

In this example we have

$$ A = $1910 ~,~ P = $1700 , t = 2 ~ \text{years} ~~ \text{and} ~ n = 1$$

After plugging the given information we have

$$ \begin{aligned} 1910 &= 1700 \left( 1 + \frac{ r }{ 1 } \right)^{\Large{ 1 \cdot 2 }} \\ 1910 &= 1700 \left( 1 + \frac{ r }{ 1 } \right)^{\Large{ 2 }} \\ \left( 1 + \frac{ r }{ 1 } \right)^{\Large{ 2 }} &= \frac{ 1910 }{ 1700 }\\ \left( 1 + \frac{ r }{ 1 } \right)^{\Large{ 2 }} &= 1.1235 ~~~ \text{ Take the natural logarithm of each side} \\ ln \left( 1 + \frac{ r }{ 1 }\right) ^{\Large{ 2 }} &= ln(1.1235) \\ 2 \cdot ln \left( 1 + \frac{ r }{ 1 }\right) &= ln(1.1235) \\ ln \left( 1 + \frac{ r }{ 1 }\right) &= \frac{ln(1.1235)}{ 2} \\ ln \left( 1 + \frac{ r }{ 1 }\right) &= 0.0582 \\ 1 + \frac{ r }{ 1 } &= e^{ 0.0582 } \\ 1 + \frac{ r }{ 1 } &= 1.0599 \\ \frac{ r }{ 1 } &= 0.0599 \\ r &= 0.0599 \approx 6\% \end{aligned}$$