- Calculators
- ::
- Financial Calculators
- ::
- Compound Interest Calculator
Compound interest calculator
Compound interest is calculated on both the initial payment and the interest earned in previous periods.
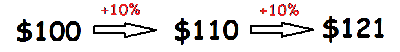
problem
How much money would you need to deposit today at 8% annual interest compounded monthly to have $1200 in the account after 12 years?
solution
The principal is $460.72.
explanation
To find amount we use formula:
| $$ A = P \left( 1 + \frac{r}{n} \right)^{\Large{n \cdot t}} $$ |
A = total amount P = principal (amount of money deposited) r = annual interest rate n = number of times compounded per year t = time in years |
In this example we have
$$ A = \$1200 ~,~ r = 8 \% ~ , ~ n = 12 ~ \text{and} ~ t = 12 ~ \text{years} $$After plugging the given information we have
$$ \begin{aligned} 1200 &= P \left( 1 + \frac{ 0.08 }{ 12 } \right)^{\Large{ 12 \cdot 12 }} \\ 1200 &= P \cdot { 1.00667 } ^ { 144 } \\ 1200 &= P \cdot 2.604631 \\ P &= \frac{ 1200 }{ 2.604631} \\ P &= 460.72 \end{aligned} $$

working...
Examples:
example 1:ex 1:
What is the value of a $4500 deposit at 7% compounded annual interest if it is held in a
bank for 9 years?
example 2:ex 2:
What will a $3500 deposit at 10% compounded
monthly be worth after 8 years in the bank?
example 3:ex 3:
How much money would you need to put today at 8% annual compounded monthly
interest to have $1200 in the account after 12 years?
example 4:ex 4:
Determine the present value of $1000 at a 12% annual interest rate compounded
quarterly at the end of two years.
example 5:ex 5:
What is the estimated yearly interest rate if you give someone $1700 and get repaid
$1910 in two years?
example 6:ex 6:
Assume that a savings account with a principal of $1350 is compounded monthly.
After 8 months, the total had risen to $1424. What was the interest rate per year?
example 7:ex 7:
How long does it take $4300 to grow to $6720 when compounded quarterly at
9%?
Search our database of more than 200 calculators
Please tell me how can I make this better.
438 413 878 solved problems